贝叶斯推理与机器学习（四）概率图模型

$$ \newcommand\indep{\mathrel{\rlap{\perp}\mkern2mu{\perp}}} \newcommand\dep{\mathrel{\style{display: inline-block; transform: rotate(180deg)}{\indep}}} $$

概率图模型（Graphical Model）

两个重要应用领域中的典型模型

建模

信念网络、马尔可夫网络、链图和影响图。

推理

因子图和联结树。

马尔可夫网络（Markov Network）

与信念网络的对比

图模型	描述
信念网络	联合概率分布的因子化（几个概率分布相乘）
马尔可夫网络	$ p(a, b, c) = \frac{1}{Z} \phi(a, b) \phi(b, c) \\ \phi(a, b)\ 和\ \phi(b, c)\ 是\ 组势 \\ Z 是保证归一化的常量 $

组势（Potential）

$$ \phi(x) \ge 0 $$

概率分布是一个特殊的满足归一化的组势。

马尔可夫网络

假设我们有

$$ X = \{x_1, ..., x_n\} \\ X_c \subseteq X $$

马尔可夫网络定义为 $ X_c $ 上的组势的乘积：

$$ p(x_1, ..., x_n) = \frac{1}{Z} \prod_{c=1}^{C} \phi_c(X_c) $$

无向图 $ G $ 中每个 $ X_c, c=1, ..., C $ 是 $ G $ 的最大团。

4_1_markov_network

吉布斯分布（Gibbs Distribution）

团组势严格为正：

$$ \phi (X_c) > 0 $$

成对（Pairwise）马尔可夫网络

图只包含大小为2的团（未必是最大团），即组势只定义在两个变量上。

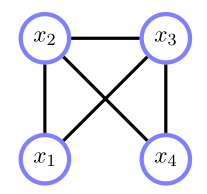
4_2_pairwise_mn

如上图，标准马尔可夫网络表示为：

$$ p(x_1, x_2, x_3, x_4) = \frac{\phi(x_1, x_2, x_3) \phi(x_2, x_3, x_4)}{Z} $$

成对马尔可夫网络表示为：

$$ p(x_1, x_2, x_3, x_4) = \frac{\phi(x_1, x_2) \phi(x_1, x_3) \phi(x_2, x_3) \phi(x_2, x_4) \phi (x_3, x_4)}{Z} $$

性质

马尔可夫网络的基本性质

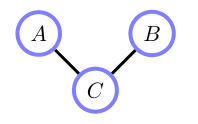
4_3_mn_property

$$ p(A, B, C) = \phi_{AC}(A, C) \phi_{BC}(B, C) / Z $$

边缘化C，使A和B（图形）相关

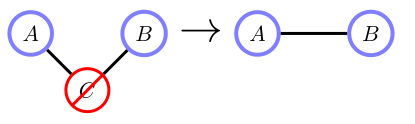
4_4_margin_on_c

一般来说， $ p(A, B) \neq p(A)p(B) $ 。

以C为条件，使A和B相互独立

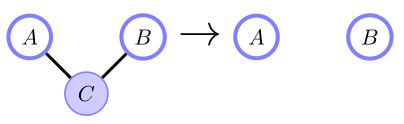
4_5_condition_on_c

$$ p(A, B|C) = p(A|C) p(B|C) $$

全局马尔可夫性质

分离

现有 $ X $ 的子集 $ S, A, B $

$ S $ 使 $ A $ 与 $ B $ 分离，当每条从 $ \forall a \in A $ 到 $ \forall b \in B $ 的路径经过 $ S $ 中的点。

如果 $ S = \emptyset $ ，则 $ a $ 到 $ b $ 之间不存在一条路径。

如果 $ a $ 到 $ b $ 之间不存在一条路径，则 $ A $ 与 $ B $ 分离。

如果 $ (A, B, S) $ 中 $ S $ 使 $ A $ 与 $ B $ 分离，则：

$$ A \indep B | S $$

例如：

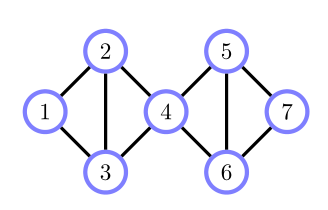
4_6_global_markov_property_1

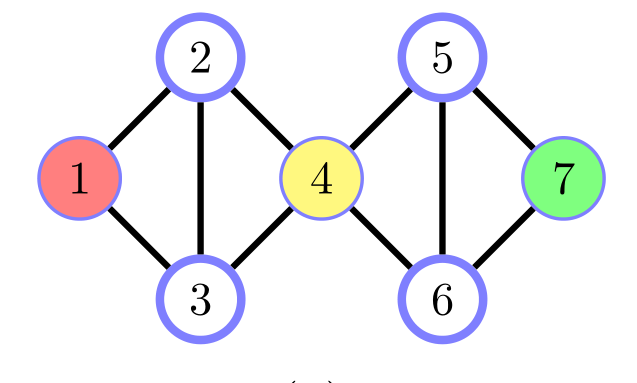
4_7_global_markov_property_2

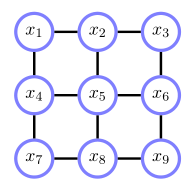
每一条从 $ 1 $ 到 $ 7 $ 的路径经过 $ 4 $ ，所以：

$$ 1 \indep 7 | 4 $$

$$ \begin{align*} p(1, 7 | 4) \propto & \sum_{2,3,5,6} p(1,2,3,4,5,6,7) \\ = & \sum_{2,3,5,6} \phi(1, 2, 3) \phi(2, 3, 4) \phi(4, 5, 6) \phi(5, 6, 7) \\ = & \left\{ \sum_{2,3} \phi(1, 2, 3) \phi(2, 3, 4) \right\}\left\{ \sum_{5, 6} \phi(4, 5, 6) \phi(5, 6, 7) \right\} \end{align*} $$

吉布斯分布（正组势）的属性

局部马尔可夫性质

$$ p(x|X \backslash x) = p(x|ne(x)) \\ ne(x) \quad x的邻居 $$

成对马尔可夫性质

$$ x \indep y | X \backslash \{x, y\} $$

马尔可夫随机场（Markov Random Field）

如果

$$ p(x_i | x_{\backslash i}) = p(x_i|ne(x_i)) \\ \left(x_{\backslash i} = X \backslash x_i\right) $$

即一个变量仅与其相邻（相连接）的变量相关；

则这个分布是一个马尔科夫随机场。

Hammersley-Clifford 定理

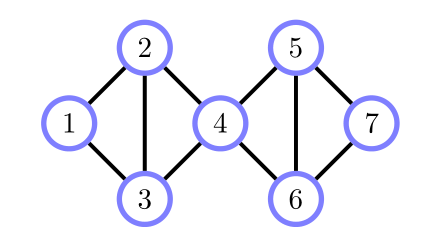
4_8_hc_theorem

由局部马尔可夫性质，可知：

$$ x_1 \indep x_4, x_5, x_6, x_7 | x_2, x_3 $$

所以，

$$ p(x_1, ..., x_7) = p(x_1 | x_2, x_3) p (x_2, x_3, x_4, x_5, x_6, x_7) $$

继续分解，最终得到：

$$ p(x_1, ..., x_7) = p(x_1 | x_2, x_3) p(x_2, x_3 | x_4) p(x_4 | x_5, x_6) p(x_5, x_6 | x_7) p(x_7) $$

Hammersley-Clifford 定理说明了这个分解性质对于所有组势为正的无向图成立。

信念网络和马尔可夫网络上的条件独立性

这里提供一个方法，来找到针对信念网络和马尔可夫网络上的，关于 $ X, Y, Z $ 的独立性描述。

对于马尔可夫网络，只需要应用最后一步（第三步）。

第一步：继承图

保留节点 $ X \cup Y \cup Z $ 和他们的祖先 $ A $ 。

移除所有其他节点，移除其他节点的入边和出边。

第二步：Moralization

连接任意两个拥有共同孩子的节点。

移除边上的箭头（变为无向图）。

第三步：分离

移除与 $ Z $ 中节点直接相连的边。

寻找一个条将 $ X $ 中任意节点与 $ Y $ 中任意节点连接的路径。

如果没有找到这样的路径，则

$$ X \indep Y | Z $$

格栅模型（Lattice Model）

4_9_lattice_model

$$ p(x_1, ..., x_9) = \frac{1}{Z} \prod_{i \sim j} \phi_{ij}(x_i, x_j) \\ i \sim j 表示在无向图中相邻的i和j的索引集合 $$

链图模型（CG：Chain Graphical Model）

同时包含有向边和无向边。

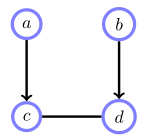
4_10_cg

$$ p(a, b, c, d) = p(a) p(b) p(c, d|a, b) $$

$$ p(c, d|a, b) = \phi(c, d) p(c|a) p(d|b) \phi(a, b) \\ 其中， \phi(a, b) = \left( \sum_{c, d} \phi(c, d)p(c|a)p(d|b) \right)^{-1} \\ \phi(a, b) 保证归一化 $$

链部件（Chain Component）

方法

移除有向边
每一个连接的部分组成一个链部件

意义

每一个链部件表示部件内变量以父部件为条件的一个条件概率分布。

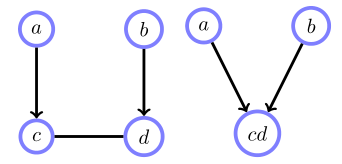
4_10_chain_component_1

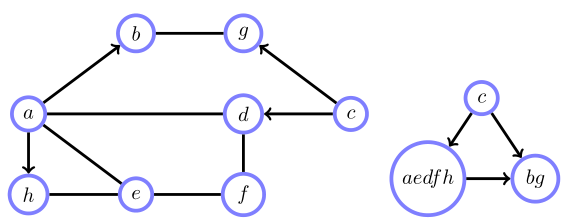
链图的概率分布

链部件集合： $ \tau $

它们对应的变量集合： $ X_t, \quad t \in \tau $

则链图的概率分布为：

$$ p(x) = \prod_{t \in \tau} p(X_t|pa(X_t)) $$

其中，

$$ p(X_t|pa(X_t)) \propto \prod_{x \in X_t} p(x|pa(x)) \prod_{c \in C_t} \phi(X_c) \\ C_t 是链部件t中所有的团的集合 $$

即父子链部件的条件概率，正比于有向边对应的父子变量的条件概率和无向边对应的一些团的组势的乘积。

特殊的链图

信念网络是链部件都是单体（只包含一个变量）的链图。

马尔可夫网络是链部件为自身的链图（若不是连通图，存在孤岛，则为每一个连接部分）

链图表达能力更强

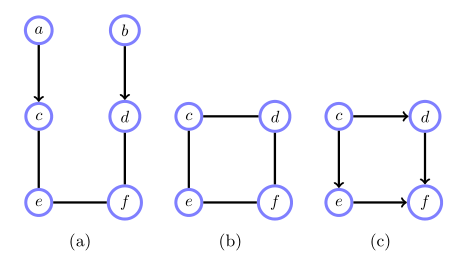
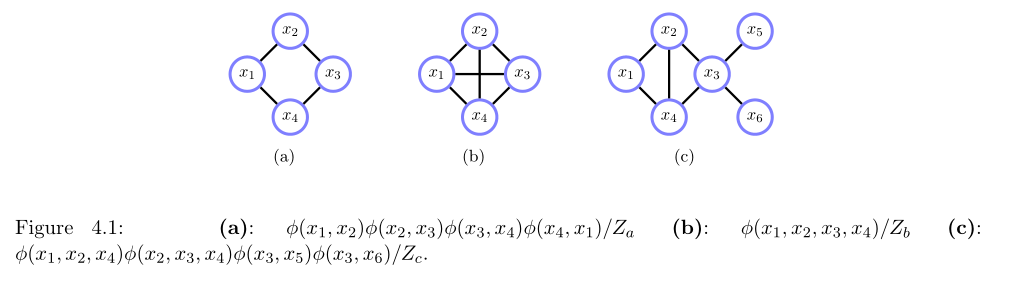
如图，

$$ (a) 表达了 a \indep b | \emptyset 和 d \indep e | (c, f) $$

没有有向图能同时表达这些条件

边缘分布 $ p(c, d, e, f) $ 是一个长为4的环构成的无向图，如图 $ (b) $ 。

将一个长为4的环，转换为有向边构成DAG（有向无环图），则一定存在一个冲突子，如图 $ (c) $ 。

没有一个连通的马尔可夫网络能够表达无条件独立

连通的马尔可夫网络无法表达：

$$ a \indep b | \emptyset $$

因子图（Factor Graph）

主要用于推理。

$$ f(x_1, ..., x_n) = \prod_i \psi_i(X_i) $$

当表示一个概率分布时：

$$ p(x_1, ..., x_n) = \frac{1}{Z}\prod_i \psi_i(X_i) $$

归一化常数 $ Z = \sum_X \prod_i \psi_i(X_i) $

图

方形节点表示 $ \psi_i $

圆形节点表示 $ x_j $

无向边连接因子 $ \psi_i $ 和变量 $ x_j $

对于一个条件概率

$$ p(x_i | pa(x_i) $$

的因子 $ \psi(X_i) $ ，我们使用由家长 $ pa(x_i) $ 指向因子节点 $ \psi(X_i) $ 的有向边，和由因子节点指向孩子 $ x_i $ 的有向边表示。

保存更多信息

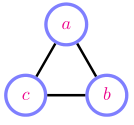
这个马尔可夫网络有两种表示方式：

$$ p(a, b, c) = \phi(a, b) \phi(a, c) \phi(b, c) = \phi(a, b, c) $$

可见马尔可夫网络会丢掉团中因式的结构信息。

但是因子图可以保留这些信息：

$$ 图(a): p(a, b, c) = \phi (a, b, c) \\ 图(b): p(a, b, c) = \phi(a, b) \phi(a, c) \phi(b, c) $$

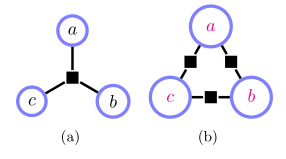
有向因子图表示信念网络

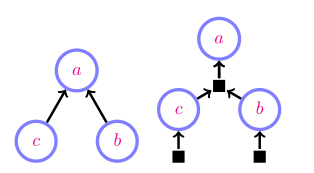
条件独立性

如果所有连接两个变量的路径被阻塞，则它们条件独立。

一条路径被阻塞，当满足下列任一条件：

路径上的一个变量在条件集合中；
路径上的一个变量或因子，有两个入边是路径的一部分（冲突子），且变量、因子和变量及因子的后代都不在条件集合中。

概率图模型的表达能力

有向分布可以被表示成无向分布

比如：

$$ p(a|b)p(b|c)p(c) $$

可以被因式化为：

$$ \phi(a, b) \phi(b, c) $$

$$ \phi(a, b) = p(a|b), \quad \phi(b, c) = p(b|c)p(c) $$

任意信念网络可以转化为马尔可夫网络

但会丢失独立性信息，还会包含额外的连接。

例如，

$$ p(c|a, b)p(a)p(b) $$

的马尔可夫网络是一个团：

$$ \phi(a, b, c) $$

通过这个团，我们不能得出信念网络中可以表达出的独立关系： $ a \indep b $ 。

独立性映射（I-Map：Independence Map）

一个图 $ G $ 是一个给定概率分布 $ P $ 的独立性映射，当：

对于所有的不交集 $ X, Y, Z $ ，有

$$ X \indep Y | Z_G \Rightarrow X \indep Y | Z_P $$

完美映射

$$ X \indep Y | Z_G \Leftrightarrow X \indep Y | Z_P $$