$$
\newcommand\indep{\mathrel{\rlap{\perp}\mkern2mu{\perp}}}
\newcommand\dep{\mathrel{\style{display: inline-block; transform: rotate(180deg)}{\indep}}}
$$
特殊证据
不确定证据(软证据)
决定了证据有多确定。
比如老奶奶对他看到的远处草坪上有一只猫只有50%的把握。
$$
\begin{align*}
y =& 有一只猫 \\
\tilde{y} =& 老奶奶看到有一只猫
\end{align*}
$$
$$ p(y|\tilde{y}) = 50\% $$
$$
p(x|\tilde{y}) = \sum_y p(x, y|\tilde{y})
= \sum_y p(x|y, \tilde{y})p(y|\tilde{y})
= \sum_y p(x|y) p(y|\tilde{y})
$$
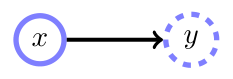
不可靠证据(似然证据)
决定了证据如何影响。
比如季节是冬天的时候,下雪的概率是80%;否则只有20%。
$$
p(G|A) \rightarrow p(H|A), \quad
其中\ p(H|A) = \left\{
\begin{array}{ll}
0.8 \quad A=tr \\
0.2 \quad A=fa
\end{array}
\right.
$$
$$ p(H|A): 虚证据 $$
信念网络(BN:Belief Network)
信念网络也叫做贝叶斯网络或贝叶斯信念网络。
$$
p(x_1, ..., x_D) = \prod_{i=1}^D p(x_i|pa(x_i)) \\
pa(x) = x的父母(parents)
$$
信念网络可表示成一个有向无环图(DAG)。
马尔可夫毯与相关性
$ x $ 的马尔可夫毯携带了所有与 $ x $ 相关的信息。
例如:
$$
MB(z_1) = {x_1, x_2, x_3, y, z_2}, \quad 则 z_1 \indep x_4 | MB(z_1)
$$
$ MB $ 即 $ MarkovBlanket $
图形相关性
信念网络可以用DAG(有向无环图)来展示,但有一些概率分布的相关性可能并不完全与图中展示的相符。
例如:
$$ Graph: A \rightarrow B, \quad 但\ p(B|A) = p(B) $$
图中显示了 $ A $ 和 $ B $ 的相关性,但事实上(根据概率的数值关系)二者相互独立。
因此,图形相关不意味着两个变量必然相关,但两个变量相关必然会在图形中表示出相关性。
冲突
冲突子
$$
路径\ P \\
在路径\ P\ 上的节点\ c \\
a\ 和\ b\ 是\ c\ 在路径\ P\ 上的邻居 \\
当 a \rightarrow c \leftarrow b, \quad c\ 是一个冲突子
$$
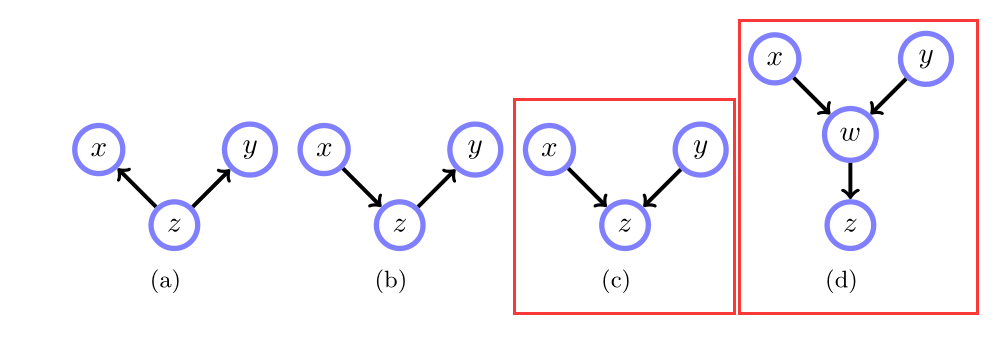
如图,只有 $ (c) $ 中的 $ z $ 和 $ (d) $ 中的 $ w $ 是冲突子。
d-连接 和 d-分离
对于每一个变量 $ x \in X $ 和 $ y \in Y $,
检查每一条 $ x $ 和 $ y $ 之间的路径 $ U $,
路径 $ U $ 被称为阻断的,当存在一个在路径 $ U $上的节点 $ w $满足下列条件之一:
-
$ w $ 是一个冲突子,且 $ w $ 及其后代都不属于 $ Z $
-
$ w $ 不是 $ U $ 上的冲突子,且 $ w \in Z $
如果所有 $ x $ 和 $ y $ 之间的路径都是阻断的,那么称 $ X $ 和 $ Y $ 是被 $ Z $ d-分离的。
否则,他们是被 $ Z $ d-连接的。
性质
如果变量集合 $ X $ 和 $ Y $ 是被 $ Z $ d-分离的,则他们在 $ Z $ 上条件独立,即:
$$ X \indep Y | Z $$
贝叶斯球(Bayes Ball)算法
给定节点集合 $ X $ 和 $ Z $,提供一个线性时间复杂度的算法,得到节点集合 $ Y $,满足
$$ X \indep Y | Z $$
Reference: Bayes Ball
马尔可夫等价类
表示相同的条件独立式集合。
判定
拥有相同的骨架以及相同的Immorality集合。
骨架
移除所有边的箭头(去除方向),剩下的就是骨架。
Immorality
是一种三个节点构成的布局。
$ A, B, C $ 满足 $ C $ 是 $ A $ 和 $ b $ 共同的孩子:
$ A \rightarrow C \leftarrow B $。
有限的表达
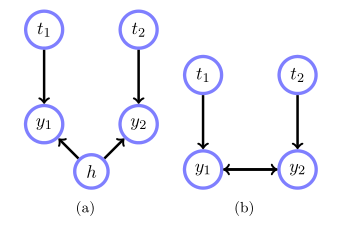
考虑上图 $ (a) $ 中的DAG,我们不能用DAG表示边缘分布:
$$ p(t_1, t_2, y_1, y_2) = p(t_1)p(t_2) \sum_h p(y_1|t_1, h) p(y_2|t_2, h)p(h) $$
因果
$$ p(a|b)p(b) = p(b|a)p(a) $$
由上式,我们可以看到两个不同的因果关系,对于条件概率而言是等价的。
严格来讲,信念网络只能表达独立性,而不是因果关系。
Simpson悖论
| 男 |
病愈者 |
未见恢复者 |
病愈率 |
| 给药 |
18 |
12 |
60% |
| 未给药 |
7 |
3 |
70% |
| 女 |
病愈者 |
未见恢复者 |
病愈率 |
| 给药 |
2 |
8 |
20% |
| 未给药 |
9 |
21 |
30% |
| 总体 |
病愈者 |
未见恢复者 |
病愈率 |
| 给药 |
20 |
20 |
50% |
| 未给药 |
16 |
24 |
40% |
分别来看男性或女性,未给药时病愈率更高;然而,总体来看,给药后病愈率反而更高。
如果这个问题的模型是这样的:
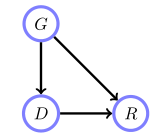
其中
$$
G:性别 \\
D:给药 \\
R:病愈
$$
那么
$$ p(G, D, R) = p(R|G, D) p(D|G) p(G) $$
但是,
$$ p(D|G) $$
事实上并不存在,实验中是否给药与患者性别无关。
所以
$$ \tilde{p}(G, R|D) = p(R|G, D) p(G) $$
$$ 我们用符号\ ||\ 表示这种干预: $$
$$
p(R||D) \equiv \tilde{p}(R|D)
= \frac{\sum_G p(R|G, D)p(G)}{\sum_{R,G} p(R|G, D)p(G)}
= \sum_G p(R|G, D)p(G)
$$
由上可知,总体情况不能像表格中那样计算:
$$
\begin{align*}
p(病愈|给药) =& p(病愈||给药) \\
=& \sum_{性别} p(病愈|性别, 给药)p(性别) \\
=& p(病愈|男, 给药)p(男) + p(病愈|女, 给药)p(女) \\
=& 0.6 \times 0.5 + 0.2 \times 0.5 \\
=& 0.4
\end{align*}
$$
$$
\begin{align*}
p(病愈|不给药) =& p(病愈||不给药) \\
=& \sum_{性别} p(病愈|性别, 不给药)p(性别) \\
=& p(病愈|男, 不给药)p(男) + p(病愈|女, 不给药)p(女) \\
=& 0.7 \times 0.5 + 0.3 \times 0.5 \\
=& 0.5
\end{align*}
$$
事实上,给药并不能提高病愈率。
$ 实际上,当性别影响给药情况的时候,即 p(D|G) 存在的时候,表格中给出的总体结果是正确的。$
总结
我们的问题是,如果给一个人吃药,会发生什么。
悖论发生,是因为我们在问一个因果(干预)问题。
“我们看到的”(观测证据)和“我们做的”(干预证据)是不同的。
我们首先进行干预,决定是否给药,然后进行观测影响,也就是病人是否病愈。
我们要对这样一个因果实验进行建模。
do-计算
$$ 观测推理:p(x|y) $$
$$ 因果推理:p(x|do(y)) $$
Pearl的do运算符
| 变量 |
表达式 |
| 所有的变量 |
$ X $ |
| 干预变量 |
$ X_C $ |
| 非干预变量 |
$ X_{\bar{C}} $ |
$$ 信念网络:p(X) = \prod_i p(X_i|pa(X_i)) $$
设置变量
$$ X_{C_1}, ..., X_{C_K}, \quad C_K \in C $$
为
$$ x_{C_1}, ..., x_{C_K} $$
的推理,等价于干预后概率分布:
$$
p(X_{\bar{C}}|do(X_{C_1} = x_{C_1}), ..., do(X_{C_K} = x_{C_K}))
= \prod_{j \in \bar{C}} p(X_j|pa(X_j))
$$
即,所有在干预集合中的变量都被设置为其干预的状态。对于干预变量,我们移除对应的条件概率项
$$ p(X_{C_i}|pa(X_{C_i})) $$
干预后概率分布还可简单表示为:
$$ p(X_{\bar{C}} || x_{C_1}, ..., x_{C_K}) $$
对于一个有因果解释的信念网络,变量的依赖顺序,必须与因果时间顺序相符。
影响图
为信念网络添加一个父决策变量 $ F_X $ 到任意一个发生干预的变量 $ X $ 上。
例如,Simpson悖论:
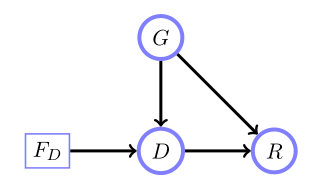
$$
\tilde{p}(D, G, R, F_D) = p(D|F_D, G) p(G) p(R|G, D) p(F_D)
$$
其中,
$$
p(D|F_D = \emptyset, G) \equiv p(D|pa(D)), \\
p(D|F_D = d, G) = \left\{
\begin{array}{ll}
1 \quad 当 D = d \\
0 \quad 其他
\end{array}
\right.
$$
影响图的优点是可以利用信念网络的一般方法来对它进行推理。





