图
包含点和边。
边的类型
有向边
边有方向,用箭头表示。有向边构成的图为有向图。
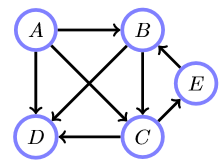
无向边
无向边构成的图为无向图。
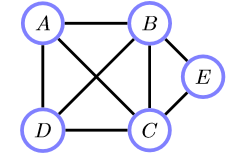
路径
祖先和后代
环
起止点相同的有向路径。
圈
不考虑边的方向(即使是有向边),起止点相同的路径(至少经过两个不同节点)。
弦
连接一个圈中两个不相邻节点的边。
是下面这个圈的一个弦
邻居
对于一个无向图,邻居用 $ ne $ 表示,
团(Clique)
对于一个无向图,团是一个全连接的节点子集。
即,团中所有成员互为邻居。
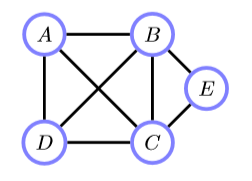
如上图中,$ \{A, B, C\} $ 是一个团。
最大团
如果不存在比当前团更大,还包含当前团的团,则当前团为最大团。
如刚才的图中,一共存在且只存在2个最大团:
小团(Cliquo)
比如图中的 $ \{A, B, C\} $ 不是最大团,则称之为小团。
全连接图
当图中任意两点间存在一条路径时,一个无向图是全连接的。(即不存在孤岛)
单连接图(Singly Connected Graph)
从任意节点 $ A $ 到任意其他节点 $ B $ 之间仅存在一条路径。
单连接图就是树(Tree)。
多连接图(Multiply Connected Graph)
若一个全连接图不是单连接的,那么就是多连接的。
生成树
一个无向图的子图,包含无向图的所有的顶点,边是无向图的边的子集,且该子图是单连接的,则称之为无向图的生成树。
有向无环图(DAG: Directed Acyclic Graph)
- 有向边。
- 没有路径会重复经过一个节点。
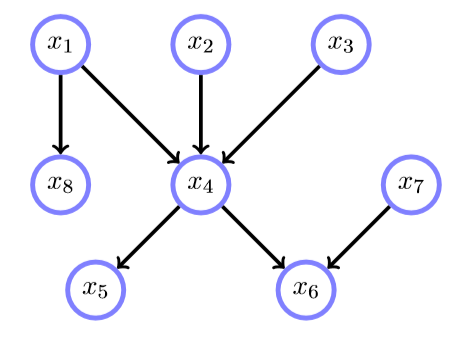
家长(Parent)
孩子(Children)
家族(Family)
节点本身及其家长。
马尔可夫毯(Markov Blanket)
节点的家长、孩子,以及孩子的其他家长(马尔可夫毯不包括节点本身)。
存储方式
边表
用列表存储节点对,表示每一条边。
无向边存储两次,表示两个方向。(无向即双向)
邻接矩阵
性质
对于一个 $ N \times N $ 的邻接矩阵,
团矩阵
对于一个无向图,它有 $ N $ 个节点,有 $ C_1, ..., C_k $ 这些最大团,
则,团矩阵是一个 $ N \times K $ 的矩阵。它的每一列表示一个最大团。
样例
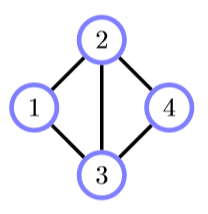
如图,有两个最大团 $ \{1, 2, 3\} 和 \{2, 3, 4\} $ 。
所以,团矩阵为:
小团矩阵
矩阵中表示的团未必是最大团。
关联矩阵
关联矩阵是一个小团矩阵,只表示由两个节点构成的团(即每条边的两个点)。可以理解成边矩阵。
上图中,存在以下由两个节点构成的团(存在以下边):
所以它的关联矩阵为:
性质
$ C_{inc}C_{inc}^T $ 除了对角线外(其对角线为每个节点的度),与邻接矩阵相同。
对于每个小团矩阵,
- 对角线上的数字
$ [CC^T]_{ii} $表示节点$ i $所在小团的数目 - 其他数字
$ [CC^T]_{ij} $表示节点$ i 和 j $共同存在的小团的数目