简述
前面几节都是在介绍回归问题,用于实现连续数据的机器学习。现在,进入分类问题,来处理离散的数据。
二元分类
回归问题中,我们的输出向量y可能是一个范围内的数值组成的向量。在二元分类问题中,只有两个值:0和1。
$$
y \in \{0, 1\}
$$
我们就先从二元分类问题入手。
分类函数
很明显,我们的分类函数满足:
$$
0 \leq h_{\theta}(x) \leq 1
$$
为便于表示和计算,采用Sigmoid函数(S型函数),也叫逻辑函数:
$$
\begin{align*}
& h_{\theta}(x) = g({\theta}^T x) \newline
& z = {\theta}^T x \newline
& g(z) = \frac{1}{1 + e^{-z}}
\end{align*}
$$
逻辑函数图像
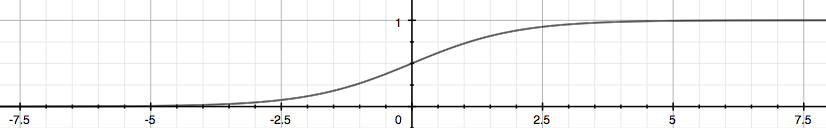
借助逻辑函数,我们可以把任意实数映射到(0, 1)的区间中,便于分类。
为了更好的理解逻辑函数,这里有个网站可以互动修改参数来预览函数图像:
含义
这样,我们得到了一个连续的函数。但在二元分类中,0和1才是我们需要的最终结果,如果函数值为0.7,有什么意义?
这个分类函数的值,实际上是给出了分类输出为1的概率。函数值为0.7,也就是说有70%的可能性,分类为1。
$$
\begin{align*}
& h_{\theta}(x) = P(y=1|x;\theta) = 1 - P(y=0|x;\theta) \newline
& P(y=0|x;\theta) + P(y=1|x;\theta) = 1
\end{align*}
$$
分类为0的可能性与分类为1的可能性互补(和为1)。
Octave/MATLAB代码
function g = sigmoid(z)
g = 1 ./ (1 .+ exp(-z));
end
function h = hypothesis(theta, X)
h = sigmoid(X * theta);
end
决策边界
有了分类函数,得到了不同分类的概率,为了得到最终分类结果,我们可以这样转换分类函数的结果:
$$
\begin{align*}
h_{\theta}(x) \geq 0.5 &\to y = 1 \newline
h_{\theta}(x) < 0.5 &\to y = 0
\end{align*}
$$
将逻辑函数代入,可得:
$$
\begin{align*}
& h_{\theta}(x) = g(z) \geq 0.5 \newline
& 当 z \geq 0
\end{align*}
$$
其中
$$
z = \theta^T x
$$
所以
$$
\begin{align*}
{\theta}^Tx \geq 0 &\Rightarrow y = 1 \newline
{\theta}^Tx < 0 &\Rightarrow y = 0
\end{align*}
$$
可见,决策边界即分隔$y = 0$和$y = 1$的直线。
示例
$$
\begin{align*}& \theta = \begin{bmatrix}6 \newline -2 \newline 0\end{bmatrix} \newline & y = 1 \; 当 \; 6 + (-2) x_1 + 0 \cdot x_2 \geq 0 \newline & 6 - 2 x_1 \geq 0 \newline & - 2 x_1 \geq -6 \newline& x_1 \leq 3 \newline \end{align*}
$$
这个例子中,$x1=3$这条竖直的直线为决策边界。
在其左边有$y=1$,分类为1;在其右边有$y=0$,分类为0。
代价函数
在分类问题中,代价函数也与回归问题中的不同。这是因为,在使用逻辑函数后,再用平方差去计算代价的话,会使得代价函数起伏波动,也就不是一个凸函数。这样我们就没有办法利用梯度下降法求解最低点(只能找到一个极小值点,但由于波动,不能保证其为最小值点)。
所以,我们利用对数函数,将代价函数定义为:
$$
\begin{align*}& J(\theta) = \dfrac{1}{m} \sum_{i=1}^m \mathrm{Cost}(h_\theta(x^{(i)}),y^{(i)}) \newline & \mathrm{Cost}(h_\theta(x),y) = -\log(h_\theta(x)) \; & \text{当 y = 1} \newline & \mathrm{Cost}(h_\theta(x),y) = -\log(1-h_\theta(x)) \; & \text{当 y = 0}\end{align*}
$$
其图像大概是这样的:
y = 1时
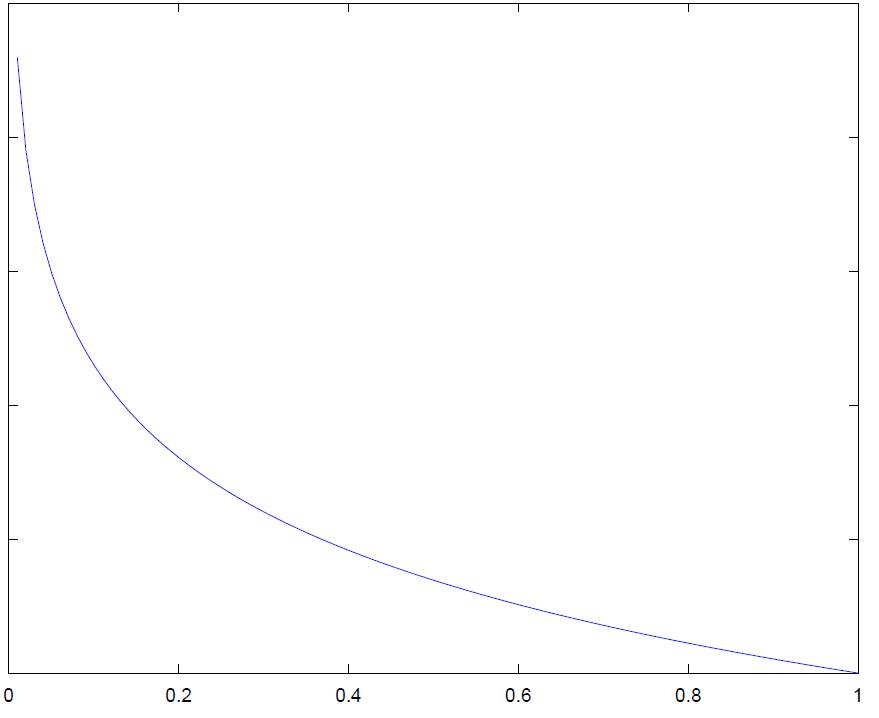
y = 0时
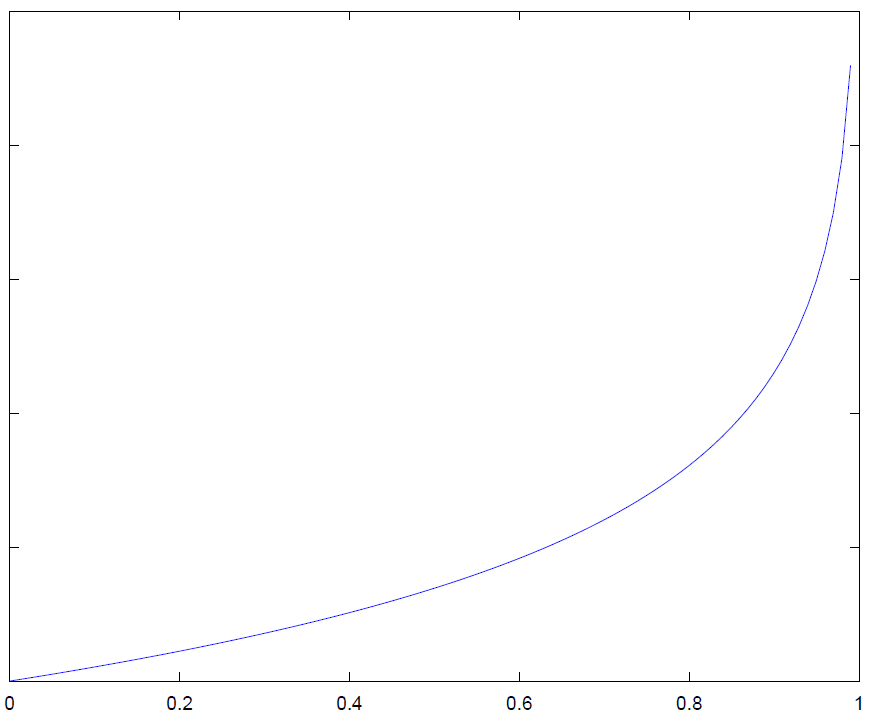
Octave/MATLAB代码
代码中涉及下一节中简化的代价函数和梯度计算。
function [J, grad] = costFunction(theta, X, y)
m = length(y); % number of training examples
h = sigmoid(X * theta);
J = 1 / m * (-y' * log(h) - (1 - y)' * log(1 - h));
grad = 1 / m * X' * (h - y);
end