多类分类问题
前面我们都是说的二元分类问题,如果数据具有多个类别该怎么办呢?比如天气情况:晴天、多云、小雨、中雨……
我们可以想到,直接做出一个分类函数,划分出所有分类的分界线,然后每一部分是一个分类。
但是,这样做,对分类函数要求太高。首先,次数高,计算代价大;其次重叠情况多,不易控制,很难实现。
于是,我们可以采用一对多的方法。
一对多
假设我们有n+1个分类(从0到n),那么我们可以将其划分成n+1个二元分类问题:
$$
\begin{align*}& y \in \lbrace0, 1 ... n\rbrace \newline& h_\theta^{(0)}(x) = P(y = 0 | x ; \theta) \newline& h_\theta^{(1)}(x) = P(y = 1 | x ; \theta) \newline& \cdots \newline& h_\theta^{(n)}(x) = P(y = n | x ; \theta) \newline& \mathrm{估值} = \max_i( h_\theta ^{(i)}(x) )\newline\end{align*}
$$
这相当于我们对每一种分类结果的可能性进行估计,最终选择最有可能的分类。这样就可以应用之前二元分类的方法,轻松解决多类分类问题。
正规化
过拟合问题
我们知道欠拟合问题,就是说我们的回归函数或分类函数预测的值与实际偏差太大。这一般是特征值太单一造成的。
那么过拟合问题,就是对样本数据过分拟合,却丧失了一般性,不能对其他实际数据做出准确地预测。
我们看两个例子:
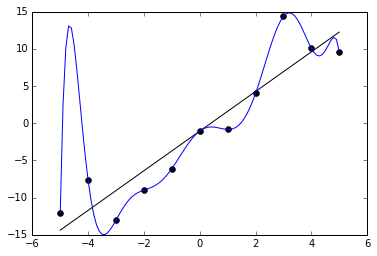
上图中,黑色的直线是对样本数据的比较好的拟合,可以较为准确的拟合样本数据,并不失一般性,可以做出预测;
但蓝色的拟合曲线则出现了过拟合问题,虽然对样本数据做到了100%的拟合度,却失掉了一般性,无法拟合新数据,从而无法做出准确预测。
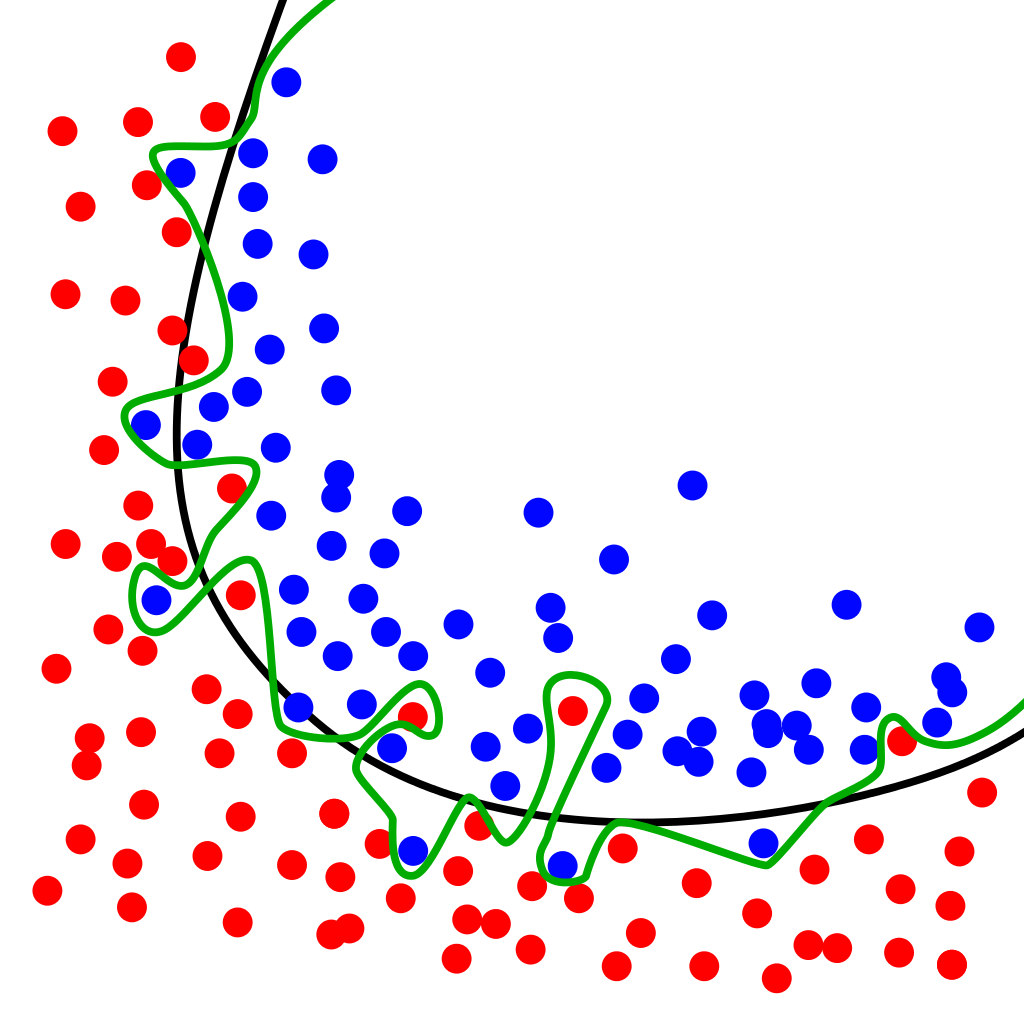
上图中展示了二元分类中可能出现的过拟合问题。
黑色的曲线较好的拟合了二元分类的决策边界;
而绿色的曲线出现了过拟合的问题,也是对样本数据做出了精确拟合,却失掉了一般性,不能保证较好的预测准确性。
解决方案
- 减少特征数量
- 手动筛选特征
- 使用模型选择算法(以后会提到)
- 正规化
- 保留所有特征,但减小(高次)参数值
$\theta_j$
代价函数
假设我们要用四次曲线做拟合:
$$
\theta_0 + \theta_1x + \theta_2x^2 + \theta_3x^3 + \theta_4x^4
$$
但又想减少3次项$ \theta_3x^3 $和4次项$ \theta_4x^4 $的影响,我们就可以将代价函数写作:
$$
J(\theta)=\dfrac{1}{2m}\sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2 + 1000\cdot\theta_3^2 + 1000\cdot\theta_4^2
$$
或者我们可以同时减小所有的参数值:
$$
J(\theta)= \dfrac{1}{2m}\ \left[ \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2 + \lambda\ \sum_{j=1}^n \theta_j^2 \right]
$$
$\lambda$是正规参数,决定了参数值增大的代价,从而抑制了过拟合。当然,如果正规参数取值过大,也会导致欠拟合问题。当其为正无穷时,回归函数成为一条水平直线。
正规化线性回归
梯度下降
$$
\begin{align*}
& \text{重复执行}\ \lbrace \newline
& \ \ \ \ \theta_0 := \theta_0 - \alpha\ \frac{1}{m}\ \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})x_0^{(i)} \newline
& \ \ \ \ \theta_j := \theta_j - \alpha\ \left[ \left( \frac{1}{m}\ \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)} \right) + \frac{\lambda}{m}\theta_j \right] &\ \ \ \ \ \ \ \ \ \ j \in \lbrace 1,2...n\rbrace\newline
& \rbrace
\end{align*}
$$
我们要把$\theta_0$单独拿出来,因为我们并不想惩罚它的增长。
可以对上面的式子进行形式转换:
$$
\theta_j := \theta_j(1 - \alpha\frac{\lambda}{m}) - \alpha\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)}
$$
可以看到,右面第二项与以前一样,而右面第一项$ 1 - \alpha\frac{\lambda}{m}$ 是一个恒小于1的数,所以每次更新,$\theta_j$的值都将一定程度的减小。
正规方程
$$
\begin{align*}& \theta = \left( X^TX + \lambda \cdot L \right)^{-1} X^Ty \newline& \text{其中}\ \ L = \begin{bmatrix} 0 & & & & \newline & 1 & & & \newline & & 1 & & \newline & & & \ddots & \newline & & & & 1 \newline\end{bmatrix}\end{align*}
$$
我们在括号中加一项以正规参数为系数的矩阵。这个矩阵除了第一个元素为0外,正对角线全为1。这样就可以实现对$\theta_0$以外的参数$\theta_j$的值的抑制。
正规化逻辑回归
代价函数
先回忆一下逻辑回归的代价函数:
$$
J(\theta) = - \frac{1}{m} \sum_{i=1}^m \large[ y^{(i)}\ \log (h_\theta (x^{(i)})) + (1 - y^{(i)})\ \log (1 - h_\theta(x^{(i)})) \large]
$$
我们只需同样在它的后面加上一项:
$$
J(\theta) = - \frac{1}{m} \sum_{i=1}^m \large[ y^{(i)}\ \log (h_\theta (x^{(i)})) + (1 - y^{(i)})\ \log (1 - h_\theta(x^{(i)}))\large] + \frac{\lambda}{2m}\sum_{j=1}^n \theta_j^2
$$
梯度下降
$$
\begin{align*}& \text{重复执行}\ \lbrace \newline& \ \ \ \ \theta_0 := \theta_0 - \alpha\ \frac{1}{m}\ \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})x_0^{(i)} \newline& \ \ \ \ \theta_j := \theta_j - \alpha\ \left[ \left( \frac{1}{m}\ \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)} \right) + \frac{\lambda}{m}\theta_j \right] &\ \ \ \ \ \ \ \ \ \ j \in \lbrace 1,2...n\rbrace\newline& \rbrace\end{align*}
$$
与线性回归形式一样。

