非线性预测
对一个拥有很多特征的复杂数据集进行线性回归是代价很高的。比如我们对50 * 50像素的黑白图分类,我们就拥有了2500个特征。如果我们还要包含所有二次特征,复杂度为$ \mathcal{O}(n^2/2) $,也就是说一共要有$ 2500^2 / 2 = 3125000 $个特征。这样计算的代价是高昂的。
人工神经网络是对具有很多特征的复杂问题进行机器学习的一种方法。
生物神经元
人工神经网络是对生物神经网络的一种简化的模拟。那么,我们先从生物中的神经元入手,进而了解神经网络的工作方式。

- 突触前(神经元)细胞的树突或细胞体接受刺激,产生兴奋或抑制。
- 动作电位传到神经末梢,导致神经递质释放。
- 使突触后(神经元)细胞的树突或细胞体接受刺激。
人工神经网络
结构
兴奋和抑制可以分别对应1和0,用节点表示每一个神经元,神经元之间由带权轴突连接,每个节点的输入相当于树突或细胞体接受外部刺激,输出相当于轴突末梢传递信息。
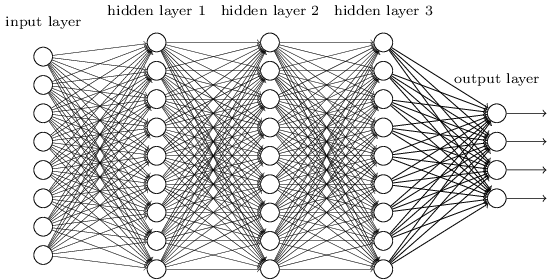
人工神经网络中的神经元为分层构造:其中第一层为输入层,最后一层为输出层,其余中间各层为隐层。
那么,人工神经网络是如何计算的呢?
总的来说,输入层接受样本特征数据,隐层之间进行计算,输出层输出最终预测结果。
而隐层之间的计算,也是一定程度上模仿了生物中的神经元。
计算描述
我们现在要计算当前神经元的值,在当前神经元所在层的前一层,有很多个突触前神经元(当前神经元也是相对于他们的突触后神经元)。
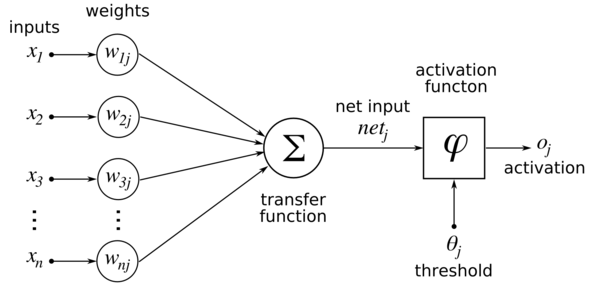
对于前一层的每一个突触前神经元,都有一个输出值,作为当前神经元的输入值,经过轴突传递到当前神经元。当然,如果是第一层神经元,则直接从输入样本数据中接受刺激(对应图中的$x_i$)。
轴突具有权值(对应图中的权值weights列:$w_{ij}$),对每一个输出值加权求和,得到该神经元的输入值。这个加权求和对应图中的transfer function(转移函数),但这个函数的名称并不明确,有人把它称作激活函数(activation function),不同的人可能有不同的叫法,这里仅供参考。
得到了该神经元的值,就要判定该神经元是否激活兴奋。这对应于图中的activation function(激活函数),但也有人将这个函数叫做输出函数(output function),而把前面说的那一部分叫做激活函数(activation function),并把这两部分合称为转移函数(transfer function)。
有几种函数可以作为激活函数:
- 阶跃函数。这是最简单直接的形式,也是人工神经网络定义时一般采用的。
- 逻辑函数。就是S型函数(Sigmoid函数),具有可无限微分的优势。
- 斜坡函数
- 高斯函数
- …
可以注意到图中的threshold(阈值),$\theta_j$,即激活阈值。也就是说,仅当神经元的值大于这个阈值时,该神经元激活兴奋,输出1;否则无法激活,输出0。
数学表述
简单一点,用符号语言描绘人工神经网络,大概就是这样:
$$
\begin{bmatrix}x_0 \newline x_1 \newline x_2 \newline \end{bmatrix}\rightarrow\begin{bmatrix}\ \ \ \newline \end{bmatrix}\rightarrow h_\theta(x)
$$
另外,我们约定几个符号标记并回忆一下逻辑函数(S型函数,Sigmoid函数):
$$
\begin{align*}& a_i^{(j)} = \text{第$j$层的第$i$个节点(神经元)的“激活值”} \newline& \Theta^{(j)} = \text{映射第$j$层到第$j+1$层的权值矩阵}\end{align*}
$$
$$ g(z) = \frac{1}{1 + e^{-z}} $$
计算过程演示
下面我们演示一下如何获得所有节点的激活值和最终的预测值。
首先假设我们的神经网络总共由3层构成,也就是:
$$
\begin{bmatrix}x_0 \newline x_1 \newline x_2 \newline x_3\end{bmatrix}\rightarrow\begin{bmatrix}a_1^{(2)} \newline a_2^{(2)} \newline a_3^{(2)} \newline \end{bmatrix}\rightarrow h_\theta(x)
$$
其中,$ x_0 $为1,作为偏移值。
然后,利用上面约定的符号,我们就可以写出所有的激活值和最终的预测值的表达式:
$$
\begin{align*}
a_1^{(2)} = g(\Theta_{10}^{(1)}x_0 + \Theta_{11}^{(1)}x_1 + \Theta_{12}^{(1)}x_2 + \Theta_{13}^{(1)}x_3) \newline
a_2^{(2)} = g(\Theta_{20}^{(1)}x_0 + \Theta_{21}^{(1)}x_1 + \Theta_{22}^{(1)}x_2 + \Theta_{23}^{(1)}x_3) \newline
a_3^{(2)} = g(\Theta_{30}^{(1)}x_0 + \Theta_{31}^{(1)}x_1 + \Theta_{32}^{(1)}x_2 + \Theta_{33}^{(1)}x_3) \newline
h_\Theta(x) = a_1^{(3)} = g(\Theta_{10}^{(2)}a_0^{(2)} + \Theta_{11}^{(2)}a_1^{(2)} + \Theta_{12}^{(2)}a_2^{(2)} + \Theta_{13}^{(2)}a_3^{(2)}) \newline
\end{align*}
$$
可见,每一层都有权值矩阵:$ \Theta^{(j)} $。其维度可以按如下规则确定:
$$
如果神经网络在第j层有s_j个节点,在第j+1层有s_{j+1}个节点,那么\Theta^{(j)}的维度是s_{j+1} * (s_j + 1)。
$$
注意,之所以是$ s_j + 1 $,是因为输入中有一个偏移节点,这里即$ x_0 $。输出的节点中则没有。
向量化表示
为了便于向量化表示,首先引入$ z_k^{(j)} $:
$$
z_k^{(2)} = \Theta_{k,0}^{(1)}x_0 + \Theta_{k,1}^{(1)}x_1 + \cdots + \Theta_{k,n}^{(1)}x_n
$$
$$
\begin{align*}a_1^{(2)} = g(z_1^{(2)}) \newline a_2^{(2)} = g(z_2^{(2)}) \newline a_3^{(2)} = g(z_3^{(2)}) \newline \end{align*}
$$
这样,可以向量化表示$x$和$z^{j}$:
$$
\begin{align*}x = \begin{bmatrix}x_0 \newline x_1 \newline\cdots \newline x_n\end{bmatrix} &z^{(j)} = \begin{bmatrix}z_1^{(j)} \newline z_2^{(j)} \newline\cdots \newline z_n^{(j)}\end{bmatrix}\end{align*}
$$
令$a^{(1)}=x$,则:
$$
z^{(j)} = \Theta^{(j-1)}a^{(j-1)}
$$
向量化计算过程
从第一层开始:
$$
z^{(j)} = \Theta^{(j-1)}a^{(j-1)}
$$
其中$\Theta^{(j-1)}$维度为$s_j * (n + 1)$($s_j$为第$j$层节点数),$a^{(j-1)}$是高为$(n+1)$的列向量。他们相乘得到一个高为$s_j$的列向量,即$z^{(j)}$。
然后,我们可以通过激活函数(这里用S型函数)得到激活值:
$$
a^{(j)} = g(z^{(j)})
$$
注意,激活函数将对向量$z^{(j)}$中每一个元素进行计算。即:
$ a_i^{(j)} = g(z_i^{(j)}) $
为了计算下一层节点的激活值,为当前层增加一个偏移量$a_0^{(j)}=1$。
重复上述过程,直到计算最后的输出层。
计算输出层前,还是一样地计算输出层前一层的输出值:
$$
z^{(j+1)} = \Theta^{(j)}a^{(j)}
$$
然后计算输出层节点的激活值,也就是最终的预测值:
$$
h_\Theta(x) = a^{(j+1)} = g(z^{(j+1)})
$$
计算过程就是这样的,可以通用于多于3层的神经网络。
示例
逻辑运算函数
人工神经网络可以用于表达一些逻辑中的常见函数:
$$
\begin{align*}AND:\newline\Theta^{(1)} &=\begin{bmatrix}-30 & 20 & 20\end{bmatrix} \newline NOR:\newline\Theta^{(1)} &= \begin{bmatrix}10 & -20 & -20\end{bmatrix} \newline OR:\newline\Theta^{(1)} &= \begin{bmatrix}-10 & 20 & 20\end{bmatrix} \newline\end{align*}
$$
其中$\Theta^{(1)}$为对应的权值矩阵。读者可以自行按照神经网络计算方法绘制逻辑真值表,看一看是不是对应的逻辑运算。
多类分类问题
上面举的例子中,输出层都只有一个节点,也就是最终的预测值$ h_{\theta} $。如果要对多类分类,可以让预测值用向量表示。此时神经网络就是这个样子的:
$$
\begin{align*}\begin{bmatrix}x_0 \newline x_1 \newline x_2 \newline\cdots \newline x_n\end{bmatrix} \rightarrow\begin{bmatrix}a_0^{(2)} \newline a_1^{(2)} \newline a_2^{(2)} \newline\cdots\end{bmatrix} \rightarrow\begin{bmatrix}a_0^{(3)} \newline a_1^{(3)} \newline a_2^{(3)} \newline\cdots\end{bmatrix} \rightarrow \cdots \rightarrow\begin{bmatrix}h_\Theta(x)_1 \newline h_\Theta(x)_2 \newline h_\Theta(x)_3 \newline h_\Theta(x)_4 \newline\end{bmatrix} \rightarrow\end{align*}
$$
最终的预测结果的形式为:
$$
h_\Theta(x) =\begin{bmatrix}0 \newline 0 \newline 1 \newline 0 \newline\end{bmatrix}
$$
我们可以对不同的向量表示不同的类别,从而做出多类分类预测。


